Human Machine Guitar Hero

Proceedings of 2024 Meaningful Play Conference

Nik Kim, "Human-Machine Guitar Hero: Developing a cooperative AI agent a human player can play with", Meaningful Play 2024 Proceedings, Pittsburgh, Apr. 2025. pp. 79-100, doi: 10.17613/z2x3h-79d21.

Play Game 🎮

Anatomy of Human-Machine Guitar Hero

HMGH regenerates Guitar Hero as a two player cooperative game. Human and machine player both thrives to earn the best socre they could achieve. Both interesting and clever twist HMGH uses is that players earn big bonus scores when each of their contribution to the total score remains roughly equally. So the player should not only work hard to play individually but also strive to distribute contribution level eqaully through out the game. Below diagram illustrates the game mechanism.

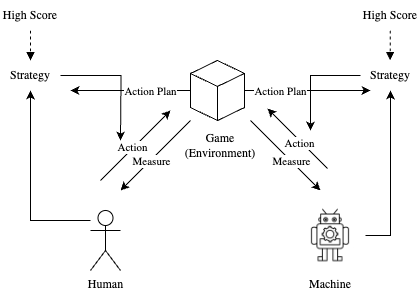
Both human and machine player interacts with the game environment. They take action toward the environment and receives feedback (measurement) about their play. Since both players' objective is to achieve higher score, each come up wi strategy. Their strategy affects their future actions as a form of action plan. Most importantly, individual's action plan broadcast to the their parter using the game system.

Engineering Details

Computing Human Player's Technical Skill Level

We need two materials to plot decision quadrant, player's skill level and management level. Let's first talk about some mathematics behind computing human player's skill level. Raw skill level is determined with three sources, total score that human player earned, the number of faulty play, lastly the number of missed shots. Put these into basic formula:

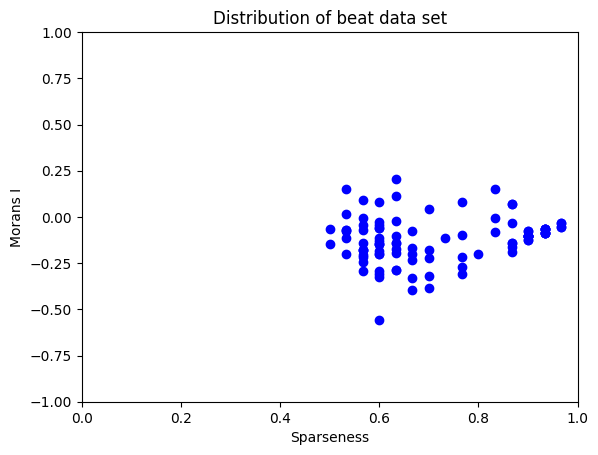
let raw_skill = (this.phumanScore - fault_weight * this.humanFault) / (this.phumanScore + humanMiss);

However, I processed this raw_skill value once again by weighting the result with difficulty of the pattern the player played. And there are some interesting idea going under computing difficulty, which is sparseness and Moran's I of given binary matrix.

• Sparseness

In HMGH scenarios, beats have either 0 or 1. 0 indicates there is no beat to play and 1 indicates there is a beat to play. In other words, patterns can be represented as binary matrix. Sparseness of 0 or 1 pattern matrix is directly connected to the perceived difficulty, since dense matrix means player is busy playing multiple beats while in sparse matrix player have more time to play beats in a timely manner.

Since we are using binary matrix, computing sparseness is simply done by using count_nonzero method from numpy library

sparseness = 1.0 - np.count_nonzero(binary_array) / binary_array.size

• Moran's I

In definition, Moran's I mean statistical measure used to assess spatial autocorrelation. The term autocorrelation sounds confusing, but it just means correlation within the data itself not in relation with different parameters. Among autocorrelation, Moran's I checks spatial auto correlation. In other words, Moran's I assesses whether similar values of a variable tend to cluster together in space, or whether they are dispersed or randomly distributed. For example, in extreme case, checker board pattern has Moran's value of -1, indicating negative spatial auto correlation. On the other hand, fully void or solid pattern has Moran's value of 1, telling positive spatial auto correlation. Moran's value around 0 indicates randomly dispersed pattern.





• Complete Difficulty Calculation

Considering both matrix sparseness and Moran's I value, final difficulty of the pattern is calculated as below:

// sparseness is converted into denseness to compute difficulty directly, range [0, 1]
denseness = 1 - sparseness
// moran's i have original range of [-1, 1] this trick is to match its range with denseness
scaled_morans_i = (1 + morans_i) / 2 
// to prevent saturation effect of multiplying two values we use squared value
difficulty = np.sqrt(denseness * scaled_morans_i)
return difficulty # range [0, 1]

• Skill Level to Mapped Skill Level

Player's raw skill level is then converted to mapped skill level taking into account pre-computed pattern difficulty. The last portion of the code represents plotting skill level on to machine's decision making quadrant.

let raw_skill_weight = 0.7;
let weighted_skill = raw_skill_weight * raw_skill + (1 - raw_skill_weight) * difficulty;
let mappedSkill = map(weighted_skill, 0, 1, 180, 460);

Computing Human Player's Management Ability

To compute the player’s management level, which measures how well they maintain equal contribution during gameplay, I tracked the total time that contribution equality was maintained. I then divided this value by the total elapsed play time. This calculation produces a score between 0 and 1.

However, the more interesting aspect lies in how I increased the difficulty of maintaining equality as the game progressed. Simply checking a fixed ratio of human and machine contributions is not sufficient. As the game continues and the accumulated score increases, it becomes easier to maintain equality within a fixed margin. For example, if 100 points have been collected and the equality window is ±5 percentage points, then a difference of just 10 points will break the equality condition. But when 1000 points are collected, the same window allows a difference of 100 points—making it less strict.

To address this, I gradually decreased the equality window as players maintained equality over time, effectively increasing the difficulty and encouraging finer control in contribution balancing.

// 1. Computing player's management level
computeHumanPlayerManagement(score) {
    let now = millis();
    let gameDuration = now - score.startTime;
    let managingAbility = score.eqDuration / gameDuration;
    let mappedManagingAbility = map(managingAbility, 0, 1, 440, 160);
    this.humanManagement.push(new Tuple(managingAbility, mappedManagingAbility));
    return mappedManagingAbility;
}
// 2. Computing equality maintained time
computeContribution() {
this.dContribution = abs(this.hContribution - this.mContribution);
let now = millis();
if (this.lastCheckedTime === 0) this.lastCheckedTime = now;
let delta = now - this.lastCheckedTime;
this.lastCheckedTime = now;

// This threshold gives dynamic equality condition as game proceeds
let threshold = max(0.5, 10 * pow(0.8, this.boost));

// Maintaining equal condition is extremely favorable to accumulate bigger bonus points
// This is because boost is increased and set by every 10s of elapsed time of eq maintanance
if (this.dContribution <= threshold) {
    if (this.savedTime === 0) {
        this.savedTime = millis();
        this.boost = 0;
    }
    this.eqDuration += delta;
} else {
    // Reset to 0
    this.savedTime = 0;
    this.boost = 0;
}

let elapsed = now - this.savedTime;
let nextBoostLevel = int(elapsed / 10000); // every 10s

if (this.savedTime !== 0 && nextBoostLevel > this.boost) {
    this.boost = nextBoostLevel;
    this.bonusTime = millis();
    this.deltaBonusPoint = (this.score * this.boost / 10) * 0.5;
    this.bonusPoint += this.deltaBonusPoint;
    }
}

This code ensures that boost tracking and equality duration are handled separately. While bonus points are triggered when equality is maintained within a 10-second interval, the total duration of equality is continuously accumulated in the variable eqDuration on every frame as long as the equality condition is met.

Audio Processing

HMGH is fundamentally a rhythm game. Therefore, generating beats corresponding to music was important. To automatically generate beat patterns that fits with music, I used python library called librosa. Librosa is a well-known python package for music and audio analysis. Specifically, I used onset detection related methods to capture new sound events during the music.

• From Digital Amplitude to Frequency-Time Data : Understanding Audio File

# Load audio file and extract amplitude and sampling rate
y, sr = librosa.load("/content/drive/MyDrive/Colab Notebooks/Roa - Escape.mp3")
# Analysis frequency component per time windows
S = librosa.stft(y)
# Convert amplitude to dB unit to match real hearing
S_db = librosa.amplitude_to_db(abs(S))





• Detecting New Sound Events

onset_env = librosa.onset.onset_strength(y=y, sr=sr)
onset_times = librosa.onset.onset_detect(onset_envelope=onset_env, sr=sr, units='time')

This is the core step that actually captures new audio events that players can respond to. To detect these moments, I used onset methods. The first method is a useful method that converts raw audio data into onset strength envelope. This enveloper shows how much the energy has increased compared to the previous frame. The last method onset_detect takes this strength envelope and returns the exact moment of the peak in energy.





• Audio magnitude data (y) into onset strength data

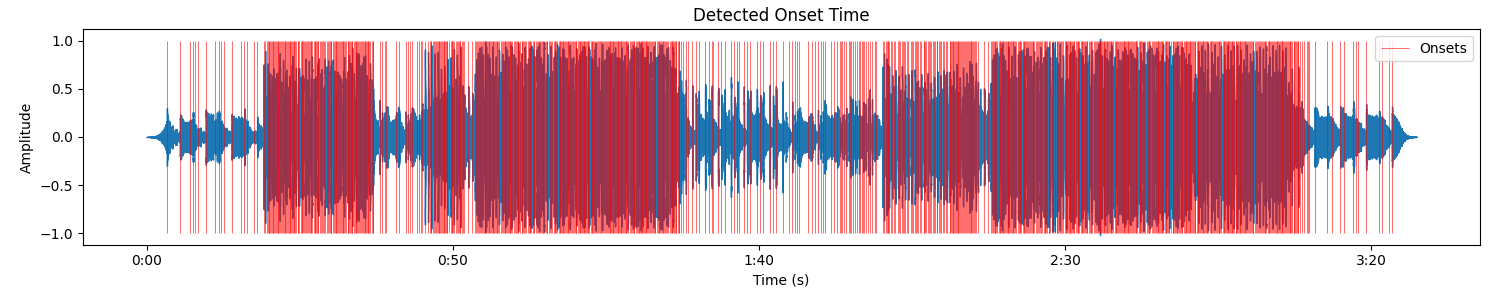
Generated onset times data is then sliced into 0.2 seconds per row, a uint of pattern forms 10 rows, which means a pattern consisting 2 seconds of play beats. Lastly each difficulty is computed using Moran's I and spareness value that we covered previously, stored as json format, that will be eventually loaded into the game scene.

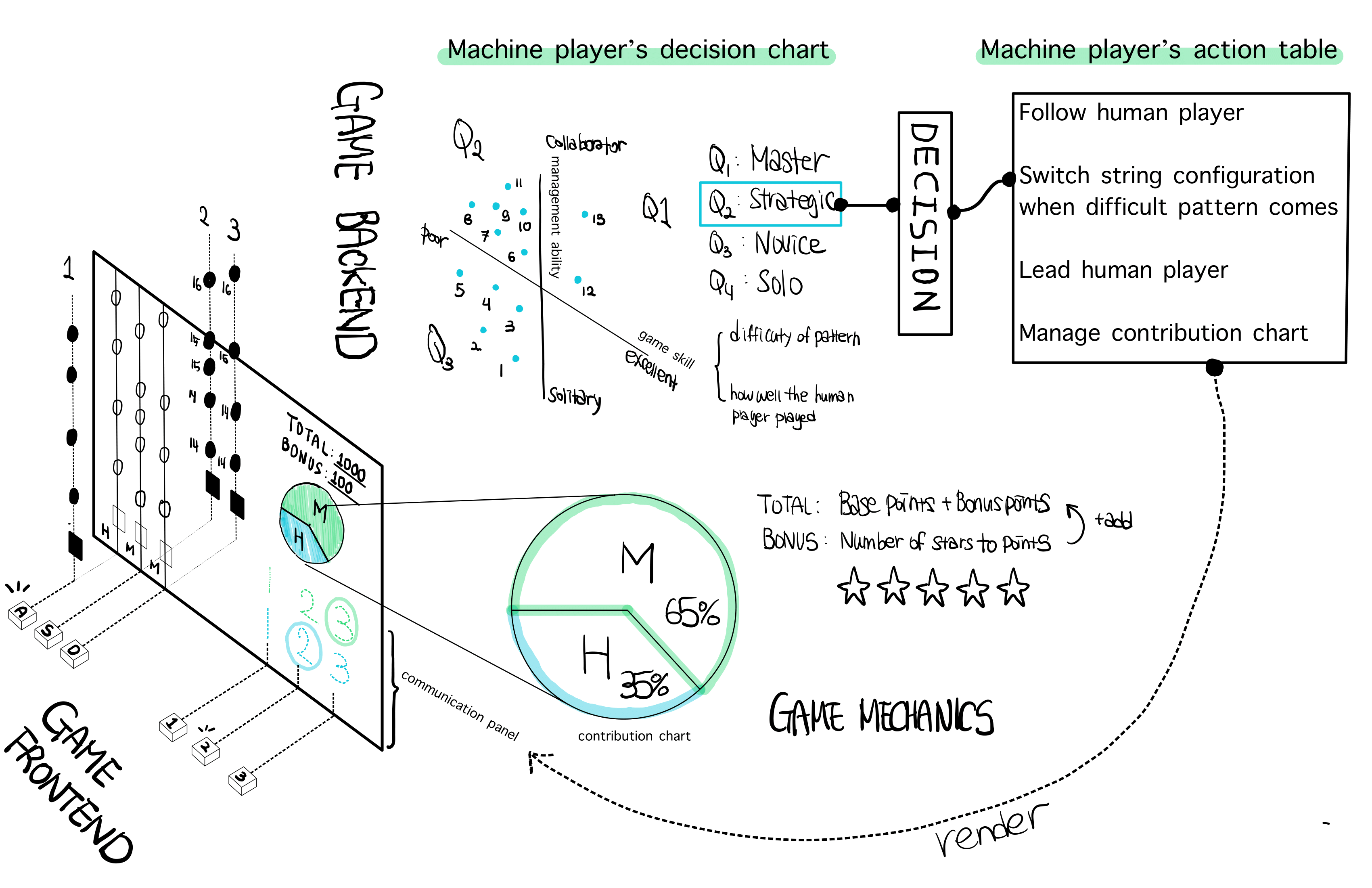
Modeling Cooperative Machines : Decision Quadrant and Action Table

The most interesting part is: “How should the gameplay be designed in terms of the machine player?” To model a machine player’s play, we should answer the following three questions. First, what to learn? Second, how to model decisions? Third, how to model actions?

What to learn?

In an ideal scenario, the machine agent would also learn and adapt to the game environment over time. However, in this prototype, the machine’s knowledge of the environment is pre-programmed—in other words, it functions as a perfect player from the outset. Instead, the focus of this project is on the second aspect: learning about its human counterpart. The machine player closely monitors the human player’s every in-game action, using this information to determine the human’s play style.

How to model decisions?

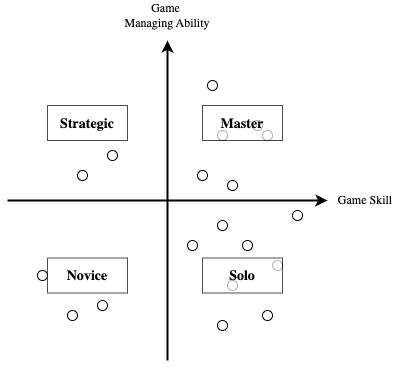
So, how can we model such decisions? Refer to Figure 3. The agent uses two numerical values to assess the human player. The skill level reflects the player’s accuracy in hitting notes at the correct timing, while the managing level represents the player’s ability to maintain a balanced contribution between the human and machine players.

Using these two dimensions, the machine maps the player’s behavior onto a playstyle quadrant. The x-axis corresponds to the skill level, and the y-axis represents the managing level. Based on the human player’s gameplay data, the machine plots the data on the quadrant and classifies human players into one of four play styles: Master, Strategic, Novice, or Solo.

How to model actions?

One last piece remains. how to model actions? Based on the previous decision, the machine player will act based on its action table, as shown in Table 1. For example, if the machine player decides the human player is a Novice, then it will change the string configuration in a way that human play is minimized. On the other hand, when the player is a Solo, then the machine will let the human player be engaged actively ensuring the contribution level is maintained. When the player is a Master, the machine will follow its counterpart’s action plan.

Supporting Conversing Systems

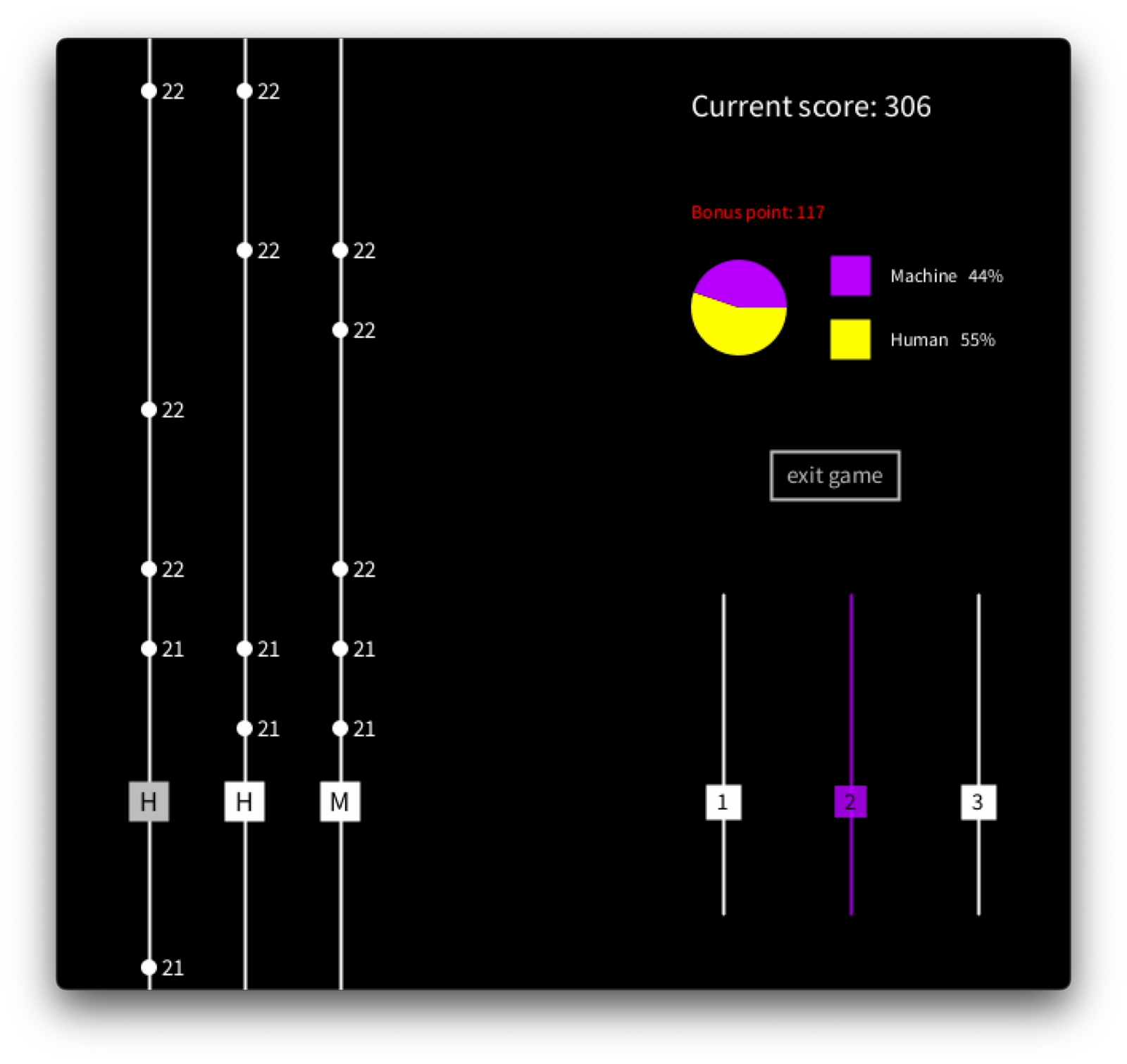
As the final component, the game must provide a means for communication between the human and machine players. This prototype supports an intuitive conversing system. In Figure 3.5a, the human player presses key 1 to indicate that they will take responsibility for string number 1. Figure 3.5b, illustrates a scenario where the machine player signals that it will take over string number 2 from the human player. In both cases, the selected string lights up with a color corresponding to the player, visually reinforcing the communication.